armi.utils.hexagon module

Generic hexagon math.

Hexagons are fundamental to advanced reactors.

armi.utils.hexagon.area(pitch)

Area of a hex given the flat-to-flat pitch.

Notes

The pitch is the distance between the center of the hexagons in the lattice.

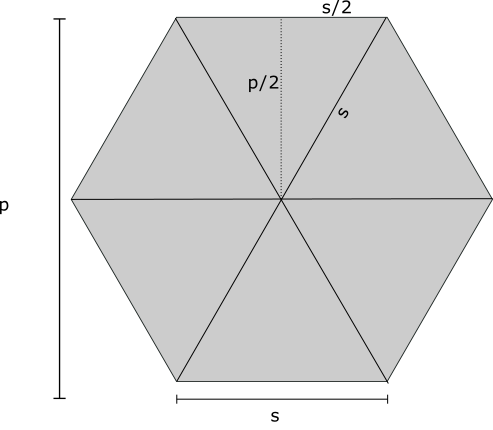
armi.utils.hexagon.side(pitch)

Side length of a hex given the flat-to-flat pitch.

Pythagorean theorem says:

\[\frac{s}{2}^2 + \frac{p}{2}^2 = s^2\]

which you can solve to find p = sqrt(3)*s

Notes

The pitch is the distance between the center of the hexagons in the lattice.

armi.utils.hexagon.corners(rotation=0)

Return the coordinates of a unit hexagon, rotated as requested.

Zero rotation implies flat-to-flat aligned with y-axis. Origin in the center.

armi.utils.hexagon.pitch(side)

Calculate the pitch from the length of a hexagon side.

Notes

The pitch is the distance between the center of the hexagons in the lattice.

armi.utils.hexagon.numRingsToHoldNumCells(numCells)

Determine the number of rings in a hexagonal grid with this many hex cells. If the number of pins don’t fit exactly into any ring, returns the ring just large enough to fit them.

Parameters:

numCells (int) – The number of hex cells in a hex lattice

Returns:

numRings – Number of rings required to contain numCells items.

Return type:

int

Notes

The first hex ring (center) holds 1 position. Each subsequent hex ring contains 6 more positions than the last. This method works by incrementing ring numbers until the number of items is reached or exceeded. It could easily be replaced by a lookup table if so desired.

armi.utils.hexagon.numPositionsInRing(ring)

Number of positions in ring (starting at 1) of a hex lattice.

armi.utils.hexagon.totalPositionsUpToRing(ring: int) → int

Return the number of positions in a hexagon with a given number of rings.

armi.utils.hexagon.getIndexOfRotatedCell(initialCellIndex: int, orientationNumber: int) → int

Obtain a new cell number after placing a hexagon in a new orientation.

Parameters:

• initialCellIndex (int) – Positive number for this cell’s position in a hexagonal lattice.

• orientationNumber – Orientation in number of 60 degree, counter clockwise rotations. An orientation of zero means the first cell in each ring of a flags up hexagon is in the upper right corner.

Returns:

New cell number across the rotation

Return type:

int

Raises:

ValueError – If initialCellIndex is not positive. If orientationNumber is less than zero or greater than five.