armi.reactor.grids.cartesian module

class armi.reactor.grids.cartesian.CartesianGrid(unitSteps=(0, 0, 0), bounds=(None, None, None), unitStepLimits=((0, 1), (0, 1), (0, 1)), offset=None, geomType='', symmetry='', armiObject=None)

Bases: StructuredGrid

Grid class representing a conformal Cartesian mesh.

It is recommended to call fromRectangle() to construct, rather than directly constructing with __init__

Notes

In Cartesian, (i, j, k) indices map to (x, y, z) coordinates. In an axial plane (i, j) are as follows:

(-1, 1) ( 0, 1) ( 1, 1)
(-1, 0) ( 0, 0) ( 1, 0)
(-1,-1) ( 0,-1) ( 1,-1)

The concepts of ring and position are a bit tricker in Cartesian grids than in Hex, because unlike in the Hex case, there is no guaranteed center location. For example, when using a CartesianGrid to lay out assemblies in a core, there is only a single central location if the number of assemblies in the core is odd-by-odd; in an even-by-even case, there are four center-most assemblies. Therefore, the number of locations per ring will vary depending on the “through center” nature of symmetry.

Furthermore, notice that in the “through center” (odd-by-odd) case, the central index location, (0,0) is typically centered at the origin (0.0, 0.0), whereas with the “not through center” (even-by-even) case, the (0,0) index location is offset, away from the origin.

These concepts are illustrated in the example drawings below.

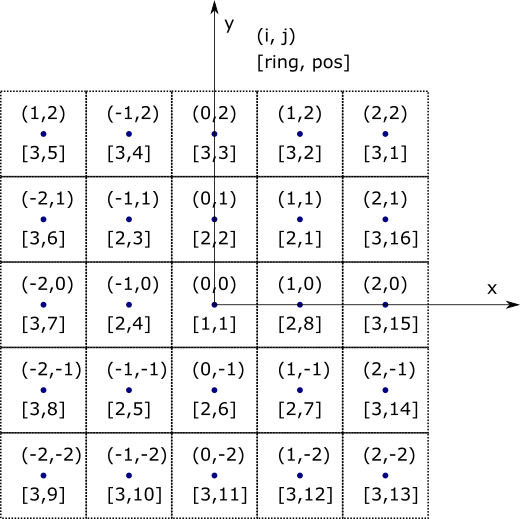
Grid example where the axes pass through the “center assembly” (odd-by-odd). Note that ring 1 only has one location in it.

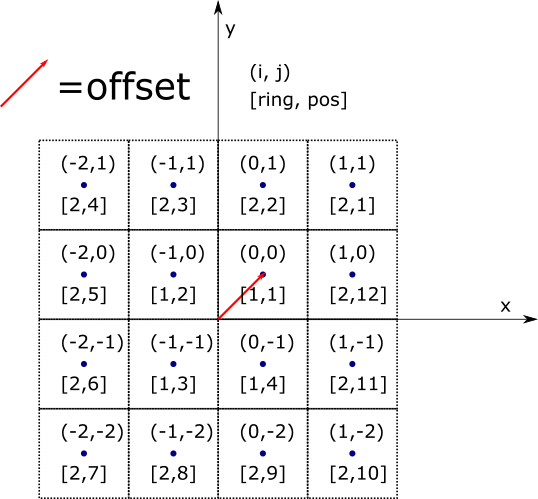
Grid example where the axes lie between the “center assemblies” (even-by-even). Note that ring 1 has four locations, and that the center of the (0, 0)-index location is offset from the origin.

classmethod fromRectangle(width, height, numRings=5, symmetry='', isOffset=False, armiObject=None)

Build a finite step-based 2-D Cartesian grid based on a width and height in cm.

Parameters:

• width (float) – Width of the unit rectangle

• height (float) – Height of the unit rectangle

• numRings (int) – Number of rings that the grid should span

• symmetry (str) – The symmetry condition (see armi.reactor.geometry)

• isOffset (bool) – If True, the origin of the Grid’s coordinate system will be placed at the bottom-left corner of the center-most cell. Otherwise, the origin will be placed at the center of the center-most cell.

• armiObject (ArmiObject) – An object in a Composite model that the Grid should be bound to.

overlapsWhichSymmetryLine(indices: Tuple[int, int]) → None

Return lines of symmetry position at a given index can be found.

Warning

This is not really implemented, but parts of ARMI need it to not fail, so it always returns None.

getRingPos(indices)

Return ring and position from indices.

Ring is the Manhattan distance from (0, 0) to the passed indices. Position counts up around the ring counter-clockwise from the quadrant 1 diagonal, like this:

7   6  5  4  3  2  1
8         |       24
9         |       23
10 -------|------ 22
11        |       21
12        |       20
13 14 15 16 17 18 19

Grids that split the central locations have 1 location in in inner-most ring, whereas grids without split central locations will have 4.

Notes

This is needed to support GUI, but should not often be used. i, j (0-based) indices are much more useful. For example:

>>> locator = core.spatialGrid[i, j, 0] # 3rd index is 0 for assembly
>>> a = core.childrenByLocator[locator]

>>> a = core.childrenByLocator[core.spatialGrid[i, j, 0]] # one liner

static getIndicesFromRingAndPos(ring: int, pos: int) → NoReturn

Not implemented for Cartesian-see getRingPos notes.

getMinimumRings(n: int) → int

Return the minimum number of rings needed to fit n objects.

getPositionsInRing(ring: int) → int

Return the number of positions within a ring.

Parameters:

ring (int) – Ring in question

Notes

The number of positions within a ring will change depending on whether the central position in the grid is at origin, or if origin is the point where 4 positions meet (i.e., the _isThroughCenter method returns True).

locatorInDomain(locator, symmetryOverlap: Optional[bool] = False)

changePitch(xw: float, yw: float)

Change the pitch of a Cartesian grid.

This also scales the offset.

getSymmetricEquivalents(indices)

property pitch: Tuple[float, float]

Grid pitch in the x and y dimension.

Returns:

• float – x-pitch (cm)

• float – y-pitch (cm)

armiObject: Optional[ArmiObject]