armi.utils.hexagon module
Generic hexagon math.
Hexagons are fundamental to advanced reactors.
- armi.utils.hexagon.area(pitch)[source]
Area of a hex given the flat-to-flat pitch.
Notes
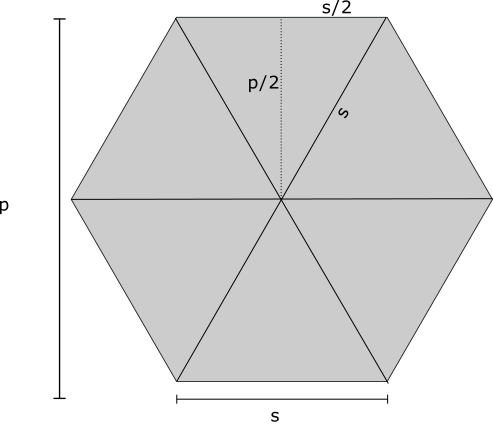
The pitch is the distance between the center of the hexagons in the lattice.
- armi.utils.hexagon.side(pitch)[source]
Side length of a hex given the flat-to-flat pitch.
Pythagorean theorem says:
\[\frac{s}{2}^2 + \frac{p}{2}^2 = s^2\]which you can solve to find p = sqrt(3)*s
Notes
The pitch is the distance between the center of the hexagons in the lattice.
- armi.utils.hexagon.corners(rotation=0)[source]
Return the coordinates of a unit hexagon, rotated as requested.
Zero rotation implies flat-to-flat aligned with y-axis. Origin in the center.
- armi.utils.hexagon.pitch(side)[source]
Calculate the pitch from the length of a hexagon side.
Notes
The pitch is the distance between the center of the hexagons in the lattice.
- armi.utils.hexagon.numRingsToHoldNumCells(numCells)[source]
Determine the number of rings in a hexagonal grid with this many hex cells. If the number of pins don’t fit exactly into any ring, returns the ring just large enough to fit them.
- Parameters:
numCells (int) – The number of hex cells in a hex lattice
- Returns:
numRings – Number of rings required to contain numCells items.
- Return type:
Notes
The first hex ring (center) holds 1 position. Each subsequent hex ring contains 6 more positions than the last. This method works by incrementing ring numbers until the number of items is reached or exceeded. It could easily be replaced by a lookup table if so desired.