armi.reactor.grids module

This contains structured meshes in multiple geometries and spatial locators (i.e. locations).

Grids are objects that map indices (i, j, k) to spatial locations (x,y,z) or (t,r,z). They are useful for arranging things in reactors, such as:

• Fuel assemblies in a reactor

• Plates in a heat exchanger

• Pins in a fuel assembly

• Blocks in a fuel assembly (1-D)

Fast reactors often use a hexagonal grid, while other reactors may be better suited for Cartesian or RZT grids. This module contains representations of all these.

Grids can be defined by any arbitrary combination of absolute grid boundaries and unit step directions.

Associated with grids are IndexLocations. Each of these maps to a single cell in a grid, or to an arbitrary point in the continuous space represented by a grid. When a Grid` is built, it builds a collection of IndexLocations, one for each cell.

In the ARMI armi.reactor module, each object is assigned a locator either from a grid or in arbitrary, continuous space (using a CoordinateLocation) on the spatialLocator attribute.

Below is a basic example of how to use a 2-D grid:

>>> grid = CartesianGrid.fromRectangle(1.0, 1.0)  # 1 cm square-pitch Cartesian grid
>>> location = grid[1,2,0]
>>> location.getGlobalCoordinates()
array([ 1.,  2.,  0.])

Grids can be chained together in a parent-child relationship. This is often used in ARMI where a 1-D axial grid (e.g. in an assembly) is being positioned in a core or spent-fuel pool. See example in armi.reactor.tests.test_grids.TestSpatialLocator.test_recursion().

The “radial” (ring, position) indexing used in DIF3D can be converted to and from the more quasi-Cartesian indexing in a hex mesh easily with the utility methods HexGrid.getRingPos() and indicesToRingPos().

This module is designed to satisfy the spatial arrangement requirements of the Reactor package.

Throughout the module, the term global refers to the top-level coordinate system while the word local refers to within the current coordinate system defined by the current grid.

class armi.reactor.grids.GridParameters(unitSteps, bounds, unitStepLimits, offset, geomType, symmetry)

Bases: tuple

Create new instance of GridParameters(unitSteps, bounds, unitStepLimits, offset, geomType, symmetry)

bounds

Alias for field number 1

geomType

Alias for field number 4

offset

Alias for field number 3

symmetry

Alias for field number 5

unitStepLimits

Alias for field number 2

unitSteps

Alias for field number 0

class armi.reactor.grids.LocationBase(i, j, k, grid)

Bases: object

A namedtuple-like object for storing location information.

It’s immutable (you can’t set things after construction) and has names.

Notes

This was originally a namedtuple but there was a somewhat unbelievable bug in Python 2.7.8 where unpickling a reactor full of these ended up inexplicably replacing one of them with an AssemblyParameterCollection. The bug did not show up in Python 3.

Converting to this class solved that problem.

property i

property j

property k

property grid

associate(grid)

Re-assign locator to another Grid.

class armi.reactor.grids.IndexLocation(i, j, k, grid)

Bases: armi.reactor.grids.LocationBase

An immutable location representing one cell in a grid.

The locator is intimately tied to a grid and together, they represent a grid cell somewhere in the coordinate system of the grid.

grid is not in the constructor (must be added after construction ) because the extra argument (grid) gives an inconsistency between __init__ and __new__. Unfortunately this decision makes whipping up IndexLocations on the fly awkward. But perhaps that’s ok because they should only be created by their grids.

detachedCopy()

Make a copy of this locator that is not associated with a grid.

See also

armi.reactor.reactors.detach

uses this

property parentLocation

Get the spatialLocator of the ArmiObject that this locator’s grid is anchored to.

For example, if this is one of many spatialLocators in a 2-D grid representing a reactor, then the parentLocation is the spatialLocator of the reactor, which will often be a CoordinateLocation.

property indices

Get the non-grid indices (i,j,k) of this locator.

This strips off the annoying grid tagalong which is there to ensure proper equality (i.e. (0,0,0) in a storage rack is not equal to (0,0,0) in a core).

It is a numpy array for two reasons:

1. It can be added and subtracted for the recursive computations through different coordinate systems

2. It can be written/read from the database.

getCompleteIndices() → Tuple[int, int, int]

Transform the indices of this object up to the top mesh.

The top mesh is either the one where there’s no more parent (true top) or when an axis gets added twice. Unlike with coordinates, you can only add each index axis one time. Thus a complete set of indices is one where an index for each axis has been defined by a set of 1, 2, or 3 nested grids.

This is useful for getting the reactor-level (i,j,k) indices of an object in a multi-layered 2-D(assemblies in core)/1-D(blocks in assembly) mesh like the one mapping blocks up to reactor in Hex reactors.

The benefit of that particular mesh over a 3-D one is that different assemblies can have different axial meshes, a common situation.

It will just return local indices for pin-meshes inside of blocks.

A tuple is returned so that it is easy to compare pairs of indices.

getLocalCoordinates(nativeCoords=False)

Return the coordinates of the center of the mesh cell here in cm.

getGlobalCoordinates(nativeCoords=False)

Get coordinates in global 3D space of the centroid of this object.

getGlobalCellBase()

Return the cell base (i.e. “bottom left”), in global coordinate system.

getGlobalCellTop()

Return the cell top (i.e. “top right”), in global coordinate system.

getRingPos()

Return ring and position of this locator.

getSymmetricEquivalents()

Get symmetrically-equivalent locations, based on Grid symmetry.

See also

Grid.getSymmetricEquivalents

distanceTo(other) → float

Return the distance from this locator to another.

class armi.reactor.grids.MultiIndexLocation(grid)

Bases: armi.reactor.grids.IndexLocation

A collection of index locations that can be used as a spatialLocator.

This allows components with multiplicity>1 to have location information within a parent grid. The implication is that there are multiple discrete components, each one residing in one of the actual locators underlying this collection.

This class contains an implementation that allows a multi-index location to be used in the ARMI data model similar to a individual IndexLocation.

detachedCopy()

associate(grid)

getCompleteIndices() → Tuple[int, int, int]

append(location: armi.reactor.grids.IndexLocation)

extend(locations: List[armi.reactor.grids.IndexLocation])

pop(location: armi.reactor.grids.IndexLocation)

property indices

Return indices for all locations.

Notes

Notice that this returns a list of all of the indices, unlike the indices() implementation for IndexLocation. This is intended to make the behavior of getting the indices from the Locator symmetric with passing a list of indices to the Grid’s __getitem__() function, which constructs and returns a MultiIndexLocation containing those indices.

class armi.reactor.grids.CoordinateLocation(i, j, k, grid)

Bases: armi.reactor.grids.IndexLocation

A triple representing a point in space.

This is still associated with a grid. The grid defines the continuous coordinate space and axes that the location is within. This also links to the composite tree.

getLocalCoordinates(nativeCoords=False)

Return x,y,z coordinates in cm within the grid’s coordinate system.

getCompleteIndices()

Top of chain. Stop recursion and return basis.

getGlobalCellBase()

getGlobalCellTop()

class armi.reactor.grids.Grid(unitSteps=(0, 0, 0), bounds=(None, None, None), unitStepLimits=((0, 1), (0, 1), (0, 1)), offset=None, geomType='', symmetry='', armiObject=None)

Bases: object

A connected set of cells characterized by indices mapping to space and vice versa.

The cells may be characterized by any mixture of regular repeating steps and user-defined steps in any direction.

For example, a 2-D hex lattice has constant, regular steps whereas a 3-D hex mesh may have user-defined axial meshes. Similar for Cartesian, RZT, etc.

Parameters

• unitSteps (tuple of tuples, optional) –

  Describes the grid spatially as a function on indices. Each tuple describes how each (x,y,or z) dimension is influenced by (i,j,k). In other words, it is:

  (dxi, dxj, jxk), (dyi, dyj, dyk), (dzi, dzj, dzk)
  

  where dmn is the distance (in cm) that dimension m will change as a function of index n.

  Unit steps are used as a generic method for defining repetitive grids in a variety of geometries, including hexagonal and Cartesian. The tuples are not vectors in the direction of the translation, but rather grouped by direction. If the bounds argument is described for a direction, the bounds will be used rather than the unit step information. The default of (0, 0, 0) makes all dimensions insensitive to indices since the coordinates are calculated by the dot product of this and the indices. With this default, any dimension that is desired to change with indices should be defined with bounds. RZtheta grids are created exclusively with bounds.

• bounds (3-tuple) – Absolute increasing bounds in cm including endpoints of a non-uniform grid. Each item represents the boundaries in the associated direction. Use Nones when unitSteps should be applied instead. Most useful for thetaRZ grids or other non-uniform grids.

• unitStepLimits (3-tuple) – The limit of the steps in all three directions. This constrains step-defined grids to be finite so we can populate them with SpatialLocator objects.

• offset (3-tuple, optional) – Offset in cm for each axis. By default the center of the (0,0,0)-th object is in the center of the grid. Offsets can move it so that the (0,0,0)-th object can be fully within a quadrant (i.e. in a Cartesian grid).

• armiObject (ArmiObject, optional) – The ArmiObject that this grid describes. For example if it’s a 1-D assembly grid, the armiObject is the assembly. Note that self.armiObject.spatialGrid is self.

Examples

A 2D a rectangular grid with width (x) 2 and height (y) 3 would be:

>>> grid = Grid(unitSteps=((2, 0, 0), (0, 3, 0),(0, 0, 0)))

A regular hex grid with pitch 1 is:

>>> grid = Grid(unitSteps= ((sqrt(3)/2, 0.0, 0.0), (0.5, 1.0, 0.0), (0, 0, 0))

Note

For this unit hex the magnitude of the vector constructed using the 0th index of each tuple is 1.0.

Notes

Each dimension must either be defined through unitSteps or bounds. The combination of unitSteps with bounds was settled upon after some struggle to have one unified definition of a grid (i.e. just bounds). A hexagonal grid is somewhat challenging to represent with bounds because the axes are not orthogonal, so a unit-direction vector plus bounds would be required. And then the bounds would be wasted space because they can be derived simply by unit steps. Memory efficiency is important in this object so the compact representation of unitSteps-when-possible, bounds-otherwise was settled upon.

Design considerations include:

• unitSteps are more intuitive as operations starting from the center of a cell, particularly with hexagons and rectangles. Otherwise the 0,0 position of a hexagon in the center of 1/3-symmetric hexagon is at the phantom bottom left of the hexagon.

• Users generally prefer to input mesh bounds rather than centers (e.g. starting at 0.5 instead of 0.0 in a unit mesh is weird).

• If we store bounds, computing bounds is simple and computing centers takes ~2x the effort. If we store centers, it’s the opposite.

• Regardless of how we store things, we’ll need a Grid that has the lower-left assembly fully inside the problem (i.e. for full core Cartesian) as well as another one that has the lower-left assembly half-way or quarter-way sliced off (for 1/2, 1/4, and 1/8 symmetries). The offset parameter handles this.

• Looking up mesh boundaries (to define a mesh in another code) is generally more common than looking up centers (for plotting or measuring distance).

• A grid can be anchored to the object that it is in with a backreference. This gives it the ability to traverse the composite tree and map local to global locations without having to duplicate the composite pattern on grids. This remains optional so grids can be used for non-reactor-package reasons. It may seem slightly cleaner to set the armiObject to the parent’s spatialLocator itself but the major disadvantage of this is that when an object moves, the armiObject would have to be updated. By anchoring directly to Composite objects, the parent is always up to date no matter where or how things get moved.

• Unit step calculations use dot products and must not be polluted by the bound indices. Thus we reduce the size of the unitSteps tuple accordingly.

Implementation: ARMI supports a number of structured mesh options. IMPL_REACTOR_MESH_0

links outgoing: REQ_REACTOR_MESH

reduce()

Return the set of arguments used to create this Grid.

This is very much like the argument tuple from __reduce__, but we do not implement __reduce__ for real, because we are generally happy with __getstate__ and __setstate__ for pickling purposes. However, getting these arguments to __init__ is useful for storing Grids to the database, as they are more stable (less likely to change) than the actual internal state of the objects.

The return value should be hashable, such that a set of these can be created.

property geomType: armi.reactor.geometry.GeomType

property symmetry: armi.reactor.geometry.SymmetryType

property offset

items()

Return list of ((i, j, k), IndexLocation) tuples.

backUp()

Gather internal info that should be restored within a retainState.

restoreBackup()

getCoordinates(indices, nativeCoords=False) → numpy.ndarray

Return the coordinates of the center of the mesh cell at the given given indices in cm.

getCellBase(indices) → numpy.ndarray

Get the mesh base (lower left) of this mesh cell in cm.

getCellTop(indices) → numpy.ndarray

Get the mesh top (upper right) of this mesh cell in cm.

locatorInDomain(locator: armi.reactor.grids.LocationBase, symmetryOverlap: Optional[bool] = False) → bool

Return whether the passed locator is in the domain represented by the Grid.

For instance, if we have a 1/3rd core hex grid, this would return False for locators that are outside of the first third of the grid.

Parameters

• locator (LocationBase) – The location to test

• symmetryOverlap (bool, optional) – Whether grid locations along the symmetry line should be considered “in the represented domain”. This can be useful when assemblies are split along the domain boundary, with fractions of the assembly on either side.

static getNeighboringCellIndices(i, j=0, k=0)

Return the indices of the immediate neighbors of a mesh point in the plane.

getSymmetricEquivalents(indices)

Return a list of grid indices that contain matching contents based on symmetry.

The length of the list will depend on the type of symmetry being used, and potentially the location of the requested indices. E.g., third-core will return the two sets of indices at the matching location in the other two thirds of the grid, unless it is the central location, in which case no indices will be returned.

static getAboveAndBelowCellIndices(indices)

cellIndicesContainingPoint(x, y=0.0, z=0.0)

Return the indices of a mesh cell that contains a point.

overlapsWhichSymmetryLine(indices)

getLabel(indices)

Get a string label from a 0-based spatial locator.

Returns a string representing i, j, and k indices of the locator

getIndexBounds()

Get min index and number of indices in this grid.

Step-defined grids would be infinite but for the step limits defined in the constructor.

Notes

This produces output that is intended to be passed to a range statement.

getBounds() → Tuple[Optional[Sequence[float]], Optional[Sequence[float]], Optional[Sequence[float]]]

Return the grid bounds for each dimension, if present.

getLocatorFromRingAndPos(ring, pos, k=0)

Return the location based on ring and position.

Parameters

• ring (int) – Ring number (1-based indexing)

• pos (int) – Position number (1-based indexing)

• k (int, optional) – Axial index (0-based indexing)

See also

getIndicesFromRingAndPos

This implements the transform into i, j indices based on ring and position.

static getIndicesFromRingAndPos(ring, pos)

Return i, j indices given ring and position.

Note

This should be implemented as a staticmethod, since no Grids currently in exsistence actually need any instance data to perform this task, and staticmethods provide the convenience of calling the method without an instance of the class in the first place.

getMinimumRings(n: int) → int

Return the minimum number of rings needed to fit n objects.

Warning

While this is useful and safe for answering the question of “how many rings do I need to hold N things?”, is generally not safe to use it to answer “I have N things; within how many rings are they distributed?”. This function provides a lower bound, assuming that objects are densely-packed. If they are not actually densely packed, this may be unphysical.

getPositionsInRing(ring: int) → int

Return the number of positions within a ring.

getRingPos(indices) → Tuple[int, int]

Get ring and position number in this grid.

For non-hex grids this is just i and j.

A tuple is returned so that it is easy to compare pairs of indices.

getAllIndices()

Get all possible indices in this grid.

buildLocations()

Populate all grid cells with a characteristic SpatialLocator.

property pitch

The pitch of the grid.

Assumes 2-d unit-step defined (works for cartesian)

class armi.reactor.grids.CartesianGrid(unitSteps=(0, 0, 0), bounds=(None, None, None), unitStepLimits=((0, 1), (0, 1), (0, 1)), offset=None, geomType='', symmetry='', armiObject=None)

Bases: armi.reactor.grids.Grid

Grid class representing a conformal Cartesian mesh.

Notes

In Cartesian, (i, j, k) indices map to (x, y, z) coordinates. In an axial plane (i, j) are as follows:

(-1, 1) ( 0, 1) ( 1, 1)
(-1, 0) ( 0, 0) ( 1, 0)
(-1,-1) ( 0,-1) ( 1,-1)

The concepts of ring and position are a bit tricker in Cartesian grids than in Hex, because unlike in the Hex case, there is no guaranteed center location. For example, when using a CartesianGrid to lay out assemblies in a core, there is only a single central location if the number of assemblies in the core is odd-by-odd; in an even-by-even case, there are four center-most assemblies. Therefore, the number of locations per ring will vary depending on the “through center” nature of symmetry.

Furthermore, notice that in the “through center” (odd-by-odd) case, the central index location, (0,0) is typically centered at the origin (0.0, 0.0), whereas with the “not through center” (even-by-even) case, the (0,0) index location is offset, away from the origin.

These concepts are illustrated in the example drawings below.

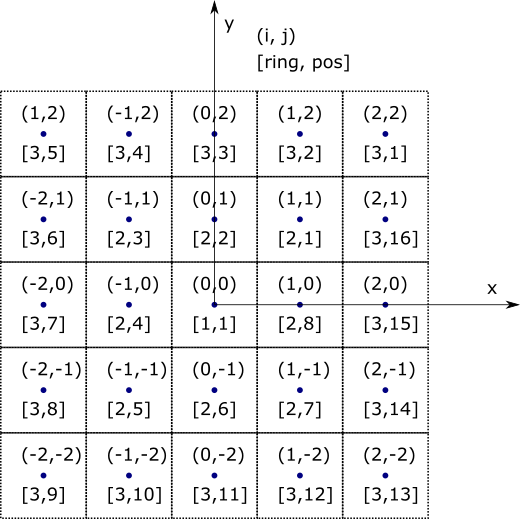
Grid example where the axes pass through the “center assembly” (odd-by-odd). Note that ring 1 only has one location in it.

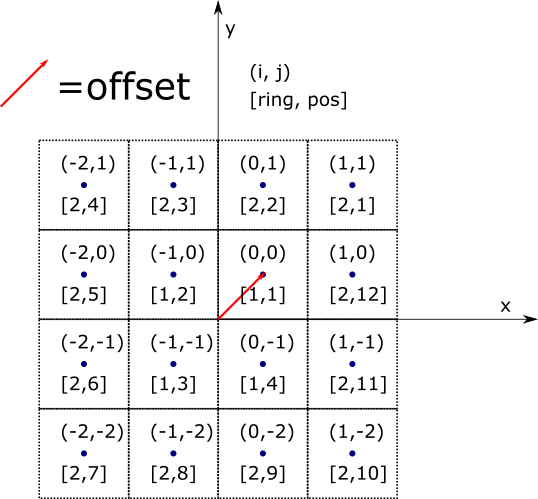
Grid example where the axes lie between the “center assemblies” (even-by-even). Note that ring 1 has four locations, and that the center of the (0, 0)-index location is offset from the origin.

Implementation: ARMI supports a Cartesian mesh. IMPL_REACTOR_MESH_1

links outgoing: REQ_REACTOR_MESH

classmethod fromRectangle(width, height, numRings=5, symmetry='', isOffset=False, armiObject=None)

Build a finite step-based 2-D Cartesian grid based on a width and height in cm.

Parameters

• width (float) – Width of the unit rectangle

• height (float) – Height of the unit rectangle

• numRings (int) – Number of rings that the grid should span

• symmetry (str) – The symmetry condition (see armi.reactor.geometry)

• isOffset (bool) – If True, the origin of the Grid’s coordinate system will be placed at the bottom-left corner of the center-most cell. Otherwise, the origin will be placed at the center of the center-most cell.

• armiObject (ArmiObject) – An object in a Composite model that the Grid should be bound to.

getRingPos(indices)

Return ring and position from indices.

Ring is the Manhattan distance from (0, 0) to the passed indices. Position counts up around the ring counter-clockwise from the quadrant 1 diagonal, like this:

7   6  5  4  3  2  1
8         |       24
9         |       23
10 -------|------ 22
11        |       21
12        |       20
13 14 15 16 17 18 19

Grids that split the central locations have 1 location in in inner-most ring, whereas grids without split central locations will have 4.

Notes

This is needed to support GUI, but should not often be used. i, j (0-based) indices are much more useful. For example:

>>> locator = core.spatialGrid[i, j, 0] # 3rd index is 0 for assembly
>>> a = core.childrenByLocator[locator]

>>> a = core.childrenByLocator[core.spatialGrid[i, j, 0]] # one liner

static getIndicesFromRingAndPos(ring, pos)

Not implemented for Cartesian-see getRingPos notes.

getMinimumRings(n)

Return the minimum number of rings needed to fit n objects.

getPositionsInRing(ring)

Return the number of positions within a ring.

Notes

The number of positions within a ring will change depending on whether the central position in the grid is at origin, or if origin is the point where 4 positions meet (i.e., the _isThroughCenter method returns True).

locatorInDomain(locator, symmetryOverlap: Optional[bool] = False)

changePitch(xw, yw)

Change the pitch of a Cartesian grid.

This also scales the offset.

getSymmetricEquivalents(indices)

class armi.reactor.grids.HexGrid(unitSteps=(0, 0, 0), bounds=(None, None, None), unitStepLimits=((0, 1), (0, 1), (0, 1)), offset=None, geomType='', symmetry='', armiObject=None)

Bases: armi.reactor.grids.Grid

Has 6 neighbors in plane.

Notes

In an axial plane (i, j) are as follows (second one is pointedEndUp):

        ( 0, 1)
 (-1, 1)       ( 1, 0)
        ( 0, 0)
 (-1, 0)       ( 1,-1)
        ( 0,-1)


    ( 0, 1) ( 1, 0)

(-1, 1) ( 0, 0) ( 1,-1)

    (-1, 0) ( 0,-1)

Implementation: ARMI supports a Hexagonal mesh. IMPL_REACTOR_MESH_2

links outgoing: REQ_REACTOR_MESH

static fromPitch(pitch, numRings=25, armiObject=None, pointedEndUp=False, symmetry='')

Build a finite step-based 2-D hex grid from a hex pitch in cm.

Parameters

• pitch (float) – Hex pitch (flat-to-flat) in cm

• numRings (int, optional) – The number of rings in the grid to pre-populate with locatator objects. Even if positions are not pre-populated, locators will be generated there on the fly.

• armiObject (ArmiObject, optional) – The object that this grid is anchored to (i.e. the reactor for a grid of assemblies)

• pointedEndUp (bool, optional) – Rotate the hexagons 30 degrees so that the pointed end faces up instead of the flat.

• symmetry (string, optional) – A string representation of the symmetry options for the grid.

Returns

A functional hexagonal grid object.

Return type

HexGrid

property pitch

Get the hex-pitch of a regular hexagonal array.

See also

armi.reactor.grids.HexGrid.fromPitch

static indicesToRingPos(i, j)

Convert spatialLocator indices to ring/position.

One benefit it has is that it never has negative numbers.

Notes

Ring, pos index system goes in counterclockwise hex rings.

getMinimumRings(n)

Return the minimum number of rings needed to fit n objects.

Notes

self is not used because hex grids always behave the same w.r.t. rings/positions.

getPositionsInRing(ring)

Return the number of positions within a ring.

getNeighboringCellIndices(i, j=0, k=0)

Return the indices of the immediate neighbors of a mesh point in the plane.

Note that these neighbors are ordered counter-clockwise beginning from the 30 or 60 degree direction. Exact direction is dependent on pointedEndUp arg.

getLabel(indices)

Hex labels start at 1, and are ring/position based rather than i,j.

This difference is partially because ring/pos is easier to understand in hex geometry, and partially because it is used in some codes ARMI originally was focused on.

static getIndicesFromRingAndPos(ring, pos)

getRingPos(indices)

Get 1-based ring and position from normal indices.

See also

getIndicesFromRingAndPos

does the reverse

overlapsWhichSymmetryLine(indices)

Return a list of which lines of symmetry this is on.

If none, returns [] If on a line of symmetry in 1/6 geometry, returns a list containing a 6. If on a line of symmetry in 1/3 geometry, returns a list containing a 3. Only the 1/3 core view geometry is actually coded in here right now.

Being “on” a symmetry line means the line goes through the middle of you.

getSymmetricEquivalents(indices)

triangleCoords(indices)

Return 6 coordinate pairs representing the centers of the 6 triangles in a hexagon centered here.

Ignores z-coordinate and only operates in 2D for now.

changePitch(newPitchCm)

Change the hex pitch.

locatorInDomain(locator, symmetryOverlap: Optional[bool] = False)

isInFirstThird(locator, includeTopEdge=False)

True if locator is in first third of hex grid.

generateSortedHexLocationList(nLocs)

Generate a list IndexLocations, sorted based on their distance from the center.

IndexLocation are taken from a full core.

Ties between locations with the same distance (e.g. A3001 and A3003) are broken by ring number then position number.

allPositionsInThird(ring, includeEdgeAssems=False)

Returns a list of all the positions in a ring (in the first third).

Parameters

• ring (int) – The ring to check

• includeEdgeAssems (bool, optional) – If True, include repeated positions in odd ring numbers. Default: False

Notes

Rings start at 1, positions start at 1

Returns

positions

Return type

int

class armi.reactor.grids.ThetaRZGrid(unitSteps=(0, 0, 0), bounds=(None, None, None), unitStepLimits=((0, 1), (0, 1), (0, 1)), offset=None, geomType='', symmetry='', armiObject=None)

Bases: armi.reactor.grids.Grid

A grid characterized by azimuthal, radial, and zeta indices.

The angular meshes are limited to 0 to 2pi radians. R and Zeta are as in other meshes.

See Figure 2.2 in Derstine 1984, ANL. [DIF3D].

Implementation: ARMI supports an RZTheta mesh. IMPL_REACTOR_MESH_3

links outgoing: REQ_REACTOR_MESH

static fromGeom(geom, armiObject=None)

Build 2-D R-theta grid based on a Geometry object.

Parameters

geomInfo (list) – list of ((indices), assemName) tuples for all positions in core with input in radians

See also

armi.reactor.systemLayoutInput.SystemLayoutInput.readGeomXML

produces the geomInfo

structure

Examples

>>> grid = grids.ThetaRZGrid.fromGeom(geomInfo)

getRingPos(indices)

static getIndicesFromRingAndPos(ring, pos)

getCoordinates(indices, nativeCoords=False)

indicesOfBounds(rad0, rad1, theta0, theta1, sigma=0.0001)

Return indices corresponding to upper and lower radial and theta bounds.

Parameters

• rad0 (float) – inner radius of control volume

• rad1 (float) – outer radius of control volume

• theta0 (float) – inner azimuthal location of control volume in radians

• theta1 (float) – inner azimuthal of control volume in radians

• sigma (float) – acceptable relative error (i.e. if one of the positions in the mesh are within this error it’ll act the same if it matches a position in the mesh)

Returns

tuple

Return type

i, j, k of given bounds

locatorInDomain(locator, symmetryOverlap: Optional[bool] = False)

ThetaRZGrids do not check for bounds, though they could if that becomes a problem.

armi.reactor.grids.axialUnitGrid(numCells, armiObject=None)

Build a 1-D unit grid in the k-direction based on a number of times. Each mesh is 1cm wide.

numCells + 1 mesh boundaries are added, since one block would require a bottom and a top.

armi.reactor.grids.locatorLabelToIndices(label: str) → Tuple[int, int, Optional[int]]

Convert a locator label to numerical i,j,k indices.

If there are only i,j indices, make the last item None

armi.reactor.grids.addingIsValid(myGrid, parentGrid)

True if adding a indices from one grid to another is considered valid.

In ARMI we allow the addition of a 1-D axial grid with a 2-D grid. We do not allow any other kind of adding. This enables the 2D/1D grid layout in Assemblies/Blocks but does not allow 2D indexing in pins to become inconsistent.